Activités de préparation pour la poursuite d'étude en BTS
Calcul algébrique 1
Développer, réduire ou factoriser une expression.
(Seconde baccalauréat professionnel. Durée 1 h)
Calcul algébrique 2
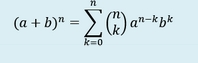
Ce document fait suite au document intitulé « calcul algébrique 1 ». L’objectif est de développer et réduire une expression de la forme (a+b)n. Ce travail s’appuie sur la formule du binôme puis sur la construction et l’utilisation du triangle de Pascal. L’élève développe sa capacité de représentation en travaillant sur le sens des calculs mis en œuvre.
(Seconde baccalauréat professionnel. Durée 1 h)
Équations du premier degré
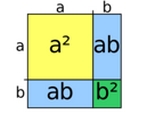
Comment résoudre algébriquement une équation du premier degré à une inconnue ? Ce document vise à développer les méthodes de résolution à disposition des élèves.
(Première baccalauréat professionnel. Durée 2 h)
Équations du second degré
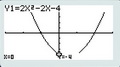
Résoudre algébriquement une équation du second degré à une inconnue.
(Première baccalauréat professionnel. Durée 2 h)
Évolution du transport intérieur routier de marchandise
Fiche élève.pdf Document TIC.ggb
Production de bouteilles

Fiche professeur.pdf Document TIC.xls
Approcher une courbe avec des droites
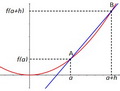
Approcher localement une courbe avec des droites.
(Première baccalauréat professionnel. Durée 2 h)
Inéquations du premier degré à une inconnue
Comment résoudre une inéquation du 1er degré à une inconnue ? Ce document vise à développer les méthodes de résolution algébriques et graphiques d’inéquations du 1er degré. La résolution d’inéquation est étendue à des inéquations de la forme A(x).B(x) < 0.
(Première et terminale baccalauréat professionnel. Durée 2 h)
Pavé dans une pyramide
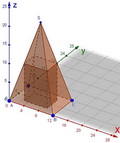
Fiche professeur.pdf Document TIC professeur.ggb Document TIC élèves.ggb
Nombre dérivé d'une fonction en a
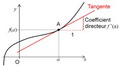
Calculer le nombre dérivé d'une fonction f en a
(Terminale baccalauréat professionnel. Durée 2 h)
Une entreprise achète une machine-outil neuve

Déterminer au bout de combien d'années la machine sera changée. Créer le tableau d'amortissement avec les TIC. Conjecturer la limite d'une suite en +∞ (Terminale baccalauréat professionnel.)


